解析屋が見た損失評価 夏休み補講編
山田 隆
(05) 形状関数の同定、でもその前に
それでは、形状関数をどのように決めていくか見ていきます。ただ、これまで、ヒステロンだの形状関数だの、物理的な意味合いが希薄になっていますので、ここで少し物理的なイメージを取り戻しにいきましょう。そのために、思い切って\(\zeta\)がゼロのヒステロン、つまり\(p_0\)だけのモデルを考えましょう。この場合、入力Hと出力\(B\)の関係を表す式(S4.6)は次のようになります。
\( B = f_0(p_0(H)) \quad \cdots \) (S4.11)
幅がゼロのヒステロン\(p_0\)は\(H\)の値をそのまま返しますので、
式(S4.11)は
\( B = f_0(H) \quad \cdots \) (S4.12)
となります。これと通常よく使われる透磁率\(m(H)\)を使った表現
\( B = \mu(H) \times H \quad \cdots \) (S4.13)
を比べてみると、関数\(f_0\)には透磁率の”ような”作用があることがわかります。これまで\(f\)は\(H\)を\(B\)に変換する、と度々言ってきたので、既にその感覚を持っていた人もいると思いますが、上のように見ればそれがより鮮明にわかると思います。
それでは、測定された材料特性から\(f\)を決めることを考えてみましょう。 これもまず、幅がゼロのヒステロンだけの場合について考えましょう。 前回のお話でfを決めるとはヒステロン上に配置された節点\(m\)の上の\(f_n(p_n,m)\)を決めればよいことを見てきました。 図S4.14を見てください。目的は\(f_n(p_n,m)\)を決めることですが、この場合、節点での\(B\)がわかればそれでおしまいです。 通常の\(BH\)の特性が測定できればおしまいです。それだけ?はい、それだけです。 プレイモデルはマイナーループが表現できますが、当然、それは通常の\(BH\)カーブの表現も内包しています。それを担っているのが幅がゼロのヒステロンだったわけです。
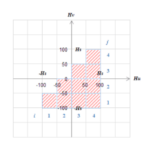
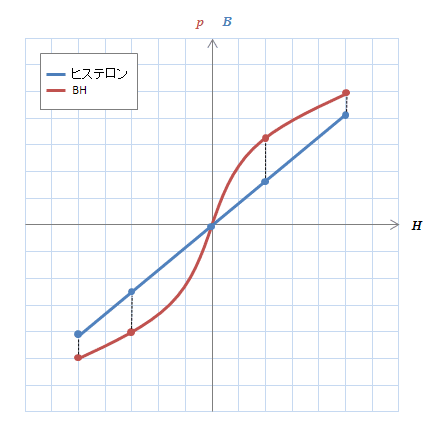 図S4.14 \(\zeta=0\)のヒステロンだけの場合の形状関数の同定
図S4.14 \(\zeta=0\)のヒステロンだけの場合の形状関数の同定節点における\(B\)の値がわかれば、節点上の形状関数\(f_0(0,m)\)の値を決めることができる。
ただ通常、プレイモデルでは\(f_n(p_n,m)\)を直接扱わず、前回の式(S4.8)に現れた\(m(n,m)\)を同定し、保持します。この\(m(n,m)\)は節点間のfの傾きですから、これを上の幅がゼロのヒステロンに当てはめると、増分透磁率がそれに相当することになります。実際の同定では\(BH\)カーブの代わりにメジャーループ群を使いますので、少々修正が必要ですが基本的な考え方は変わりません。
(06) 同定のためのメジャーループ群
では実際にヒステロンが2本以上の場合はどうなるのでしょうか?まず、使える情報を確認しておきましょう。材料特性としては振幅の異なるメジャーループ群が与えられます。それぞれのメジャーループの振幅はゼロから飽和磁界\(H_s\)[*1]までを等分割した値になるようにします(図S4.15)。その際の分割数は任意ですが、分割幅\(\Delta H\)が分解能になり、それよりも小さな幅を持つマイナーループは再現できなくなりますので注意が必要です[*2] 。通常、この分割数は数10程度にしているようです。
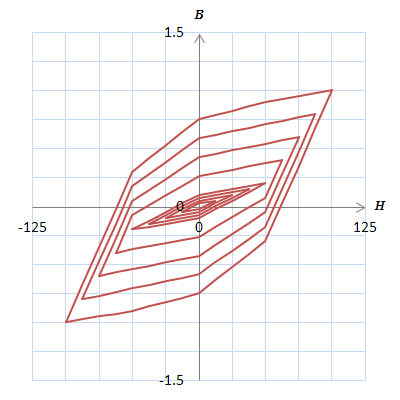 図S4.15 同定に必要なメジャーループ群の例(\(H_s=100\))
図S4.15 同定に必要なメジャーループ群の例(\(H_s=100\))最外のメジャーループの振幅は\(H_s=100\)、メジャーループの総数は8、隣り合うメジャーループの振幅の差は12.5(=100/8)になっている。
この場合のヒステロンの本数\(N_p\)は16になる。
尚、これまでにお話ししてきたヒステロンの本数\(N_p\)も、実は、このマイナーループの本数から決まります。具体的には、メジャーループの本数のちょうど2倍がヒステロンの本数\(N_p\)になります。
\( Np = メジャーループの本数 \times 2 \quad \cdots \) (S4.14)
逆に言えば、もし、ヒステロンの数を80本にしたい場合には、メジャーループを40本準備する必要があることになります。
今回は同定のための準備として、形状関数の物理的な意味と同定に必要な測定すべきメジャーループ群の説明をしました。次回は具体的に同定の作業をしてみたいと思います。
[*1] 通常のFEMでは\(B\)を入力、\(H\)を出力とするプレイモデルが使われるため、 \(B\)の振幅差が等間隔になるループ群が使われます。
[*2] 上でも述べたとおり、この解説では\(H\)入力ですが、通常のFEMでは\(B\)入力が使われます。 その際の分解能の議論は\(B\)について適用されます。