解析屋が見た損失評価 夏休み補講編
山田 隆
(12) \(K\)を材料特性から同定する方法
とにかく、式S4.23によって\(B\)が計算できてメデタシメデタシなのですが、\(K\)がわからないと具体的な計算ができません。前回の練習問題では\(K\)を1と0にしてしまいましたが、実際には、材料特性からKを同定することになります。つまり、\(K\)が材料特性を持ちます。ということで、同定方法の基本的な考え方を説明しましょう。実はこれはプレイモデルの同定方法と良く似ていて、\(B\)の変化に対応する格子の状態変化に注目して、格子\((i,j)\)のからの寄与\(K(i,j)\)を割り出していきます。尚、同定に使う材料特性のデータもプレイモデルと全く同じメジャーループ群を使います((07) 同定作業開始! 図S4.16参照)。メジャーループの数から\(H_u-H_v\)グラフの分割数\(N_q\)が決まる事情も似ていて、
\( N_p = メジャーループの数\times2 \quad \cdots \) (S4.24)
とします。ここではメジャーループの数は2としましょう。ということで\(N_q\)は4です。
動作点が一番外側のメジャーループの右上端に到達している時の\(H_u-H_v\)グラフのは図S4.27(a)のようになっています。ここから\(ΔH\)だけ\(K\)を減らします。その時、\(B\)が\(B^1_1\)から\(B^1_2\)に変化したとします。同時に、その時の\(H_u-H_v\)グラフの状態変化を見てみると格子\((4,4)\)だけが変化することがわかります(図S4.27(b))。つまり、
\( B^1_1 – B^1_2 = K(4,4) \quad \cdots \) (S4.25)
として\(K(4,4)\)を求めることができました。さらに、\(H\)を\(ΔH\)だけ下げてみましょう。そうすると、今度は\((3,3)\)と\((4,3)\)の2つが変わってしまうので、\(B\)の応答から言えるのは
\( B^1_2 – B^1_3 = K(3,3) + K(4,3) \quad \cdots \) (S4.26)
だけで、同定には至りません(図S4.27(c))。この辺りの困った感じ、何かプレイモデルの時と良く似ていますね。ということで、\(K(3,3)\)を同定するために2番目のメジャーループを使って
\( K(3,3) = B^2_1 – B^1_2 \quad \cdots \) (S4.27)
とします(図S4.27(d))。式S4.27を式S4.26に代入すると
\( K(4,3) = B^1_2 – B^1_3 -(B^2_1 – B^2_2) \quad \cdots \) (S4.28)
のように\(K(4,3)\)の同定ができました(図S4.27(e))。何だかとってもプレイモデルと良く似ています。まあ、その話は後程するとして、このようにメジャーループと\(H_u-H_v\)グラフの変化状態を見比べながら全ての\(K(i,j)\)を同定していきます。
ここまでで、プライザッハモデルの原理と同定方法について基本的ところを説明したつもりですが、理解いただけたでしょうか?今回の解説の目的はプライザッハモデルというよりもプレイモデルとの関係を示すことなので、実はここまでは準備に過ぎません。本番はこれからです。

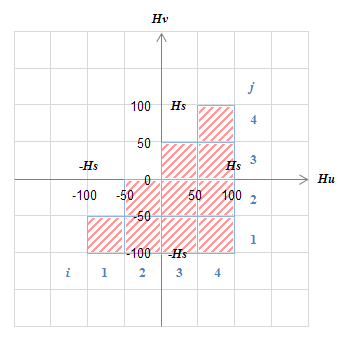 (a) 初期状態
(a) 初期状態動作点が一番外側のメジャーループの右上端にあり、すべての格子が正に磁化されている。
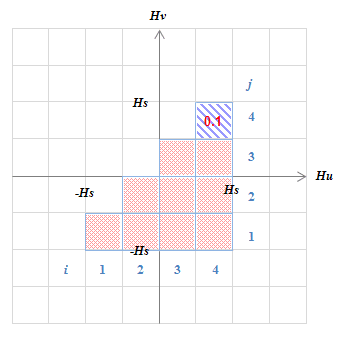 (b) 外側のメジャーループを\(H\)100から50に動かした状態
(b) 外側のメジャーループを\(H\)100から50に動かした状態\(K(4,4)\)が同定される。
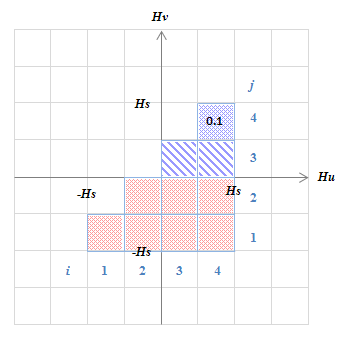 (c) 外側のメジャーループを\(H\)50から0に動かした状態
(c) 外側のメジャーループを\(H\)50から0に動かした状態磁束密度の変化は\(K(3,3)\)、\(K(4,3)\)で表現される。
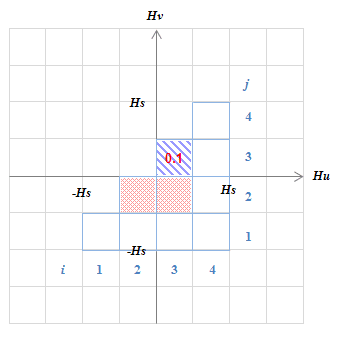 (d) 内側のメジャーループを\(H\)50から0に動かした状態
(d) 内側のメジャーループを\(H\)50から0に動かした状態\(K(3,3)\)が同定される。
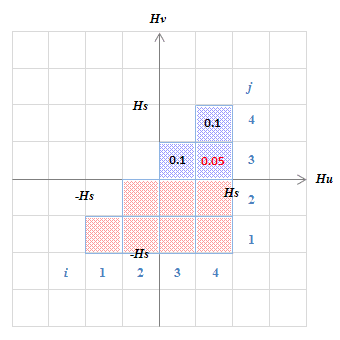 (e) 外側のメジャーループを\(H\)50から0に動かした状態
(e) 外側のメジャーループを\(H\)50から0に動かした状態(d)で\(K(3,3)\)が同定されたので、\(K(4,3)\)が同定される。