解析屋が見た損失評価
山田 隆
第4話でお話ししたアルゴリズム2の説明について、よくわからん、というコメントをいただきましたので、補足を試みたいと思います。
アルゴリズム2はヒステリシス損失計算の精度を向上させるためのものでした。それでは、渦電流損失はどうなっているのか？というのがご質問のポイントでした。
非常に的を得た問いです。その問いは既存の損失計算の限界に触れるもので、それについて考えることは次のステップへの第一歩になります。少々難しい課題なので、私が本能的に説明を避けてしまったのかもしれません。痛いところをつかれました。
ただ、渦電流損失はどうなっているか？という問いに対する回答は極めて明快で、アルゴリズム1の場合と全く同じ、です。そう言われてもあまりピンとこないかもしれません。アルゴリズム1では鉄損を一気に求めてしまい、手順として明示的に独立に渦電流損失やヒステリシス損失を求めることをしていないからです。アルゴリズム１でも二周波法に基づいた分離は可能ですが、これは全鉄損を求めた後の分離であって、全鉄損を求めるための手順ではありません。
一方、アルゴリズム2では、ヒステリシス損失\(P_{h2}\)はループを数えることによって独立に計算します。そして渦電流損失\(P_{e2}\)は全鉄損\(P_{tot}\)からヒステリシス損失\(P^*_h\)を引いた量として定義します。
\( P_{e2} = P_{tot} – P^*_h \quad \cdots \) (10)
問題はヒステリシス損失\(P_h^*\)として何を用いるか、です。何を用いるか？血迷ったのか！アルゴリズム2の改良されたヒステリシス損失\(P_{h2}\)に決まっているではないか、と思いますよね。しかし、残念ながらそうはいかないのです。ではヒステリシス損失として何を使うかと言えば、アルゴリズム1で全鉄損\(P_{tot}1\)を計算し、これを第3話で説明した方法で分離して得られるヒステリシス損失\(P_{h1}\)になります。つまり、
\( P_{e2} = P_{tot} – P_{h1} \quad \cdots \) (11)
となります。ここで\(P_{h1}\)は周波数分解によって得られる磁束密度によっていることに注意します。
ではなぜ、改良後の\(P_{h2}\)ではなく\(P_{h1}\)を使うかと言えば、式(10)の\(P_{tot}\)が周波数の関数として与えられているからです。\(P_{tot2}\)が周波数の関数であるため、式(10)は周波数毎に考える必要があります。そのため、ヒステリシス損失\(P_h^*\)も周波数の関数であることが求められます。しかし、\(P_{h2}\)は周波数の関数ではないため\(P_h^*\)になる資格がありません。苦肉の策として、周波数の関数である改良前の\(P_{h1}\)を使うことになります。結果として\(P_{e2}\)はアルゴリズム１の結果を分離して得られる渦電流損失\(P_{e1}\)と同じになります。
またなぜ\(P_{tot}\)を使うかと言えば、それが測定値であるからです。アルゴリズム2を導入した当時は、実測データをできるだけそのまま利用すべき、という考えが強くありこのような形になりました。
上でも吐露した通り、これは苦肉の策であり、理想的な方法ではありません。折角、ヒステリシス損失計算の精度を上げたにも関わらず、その効果が渦電流損失計算には及ぼすことができていません。残念です。
問題の本質は測定データの利用方法にあります。測定データの正しさはその測定条件 (単一周波数の正弦波波形) を満たした時にのみ保障されるわけですが、アルゴリズム1も2もそれを拡大解釈し、任意波形に適用したところに問題があります。これを解決するためには、もう少し第一原理に近い方法を採用する必要があります。実際、その方法も改良版として存在しており現在のJMAGでは利用可能です。それについてはコラムの後半で触れたいと思います。
お問い合わせをいただいたアルゴリズム２の渦電流損失の計算方法について説明したつもりですが、少々話が複雑になってしまったかもしれません。整理の意味も含め2つのアルゴリズムの流れを図16に載せておきます。
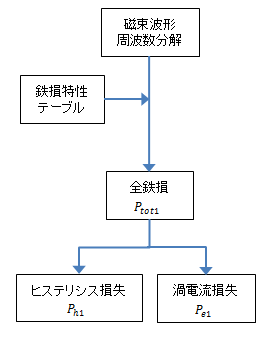(a) アルゴリズム1
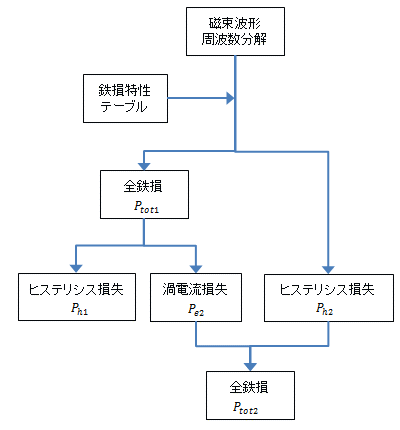(b) アルゴリズム2
図16 損失計算の流れ
また、アルゴリズム1と2が計算結果としてどのような差を出すかについても示しておきます。3つの異なる周波数の台形波と正弦波の磁束密度について、損失を計算しました。アルゴリズム1と2で得られる損失の違いをみてください(図17)。
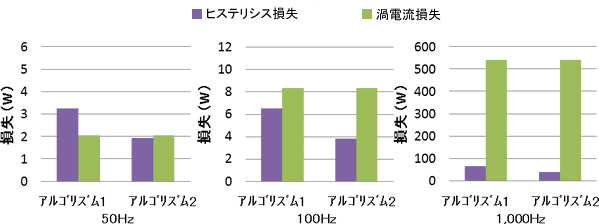(a) 台形波
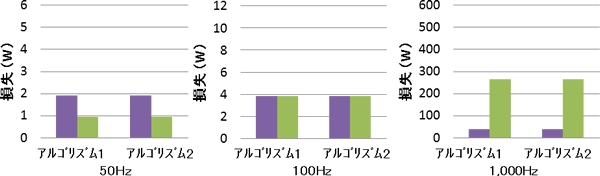(b) 正弦波
図17 アルゴリズム1と2の損失比較
これらの結果の考察についてはいずれどこかで行いたいと思います。それまで皆さんも考えてみてください。今回の件に限らず不明な点などがあれば遠慮なくお問い合わせください。
コラム後半は6/22より連載再開します。どうぞお楽しみに。
