解析屋が見た損失評価 夏休み補講編
山田 隆
(11) 分布関数の導入と磁化総量の計算
前回のお話で、プライザッハモデルが磁化反転のタイミングが異なる磁気モーメントの集合で表現されていること、その磁気モーメントの様子を把握するために\(H_u-H_v\)グラフが使われること、を説明しました。今回はそれらを使って磁化を計算できるようにし、プライザッハモデルを完成させましょう。
プライザッハモデルでは磁化特性つまり磁化総量\(M\)を求めるために、動作点における磁気モーメントを足し合わせるのですが、これを\(H_u-H_v\)グラフ上で見通し良く行うために、各点\((H_u,H_v)\)に対応する磁気モーメントの磁化総量への寄与度を表す分布関数\(K(i,j)\)というものを導入します。これを使うと磁化総量\(M\)は次のように正に磁化している格子についての\(K\)の足し算になります。
\( M = \displaystyle \sum K(i,j)\), (正に磁化している格子\(i,j\)について) \(\quad \cdots \) (S4.20)
足し算は簡単ですが、”正に磁化している領域について”というのが曲者ですね。実はここで\(H_u-H_v\)グラフの本領発揮です。格子毎の磁化状態を記憶させる入れ物を準備します。これを\(D(i,j)\)とし、次のように値を設定します。
\( D(i,j) = \begin{eqnarray} \left\{ \begin{array}{l} 1; 正に磁化している場合 \\ 2; 負に磁化している場合 \end{array} \right.\end{eqnarray}\quad \cdots \) (S4.21)
つまり、格子(\(i,j\))の磁化状態に応じて\(D(i,j)\)の値はパタパタと変わることになります。その様子を、入力が\(-H_s→H_s→0\)の場合について見てみましょう(図S4.24)。初期状態として全ての磁気モーメントは負に磁化されているとします(図S4.24(a))。つまり、全領域でDを0にします。磁界\(H\)が増える時には動作点は\(H_u\)軸(横軸)に向かって動きます(図S4.24(b))。注目している動作点\(H\)の左側の領域の磁気モーメントは全て正に反転しますので、それに対応する格子のDを1にします。磁界\(H\)を減らす時には\(H_v\)軸(縦軸)に沿って動きます(図S4.24(c))。今度は動作点\(H\)の上側の領域の磁気モーメントは全て負に反転し、そこの\(D\)を1から0にします。磁界を減らす時に\(H_u\)軸に沿って動いたり、増やす時に\(H_v\)軸に沿って動くことはないので注意してください。
このように操作をすれば動作点毎の磁化状態は\(D\)を見れば一目瞭然[*1]で、\(D\)が1の格子について式(S4.20)の足し算をすればよいことになります。もう少し、スマートにやるには、式(S4.20)を
\( M = \displaystyle \sum_{ 1 \leq i \leq B \\ 1 \leq j \leq i} K(i,j) * D(i,j) \quad \cdots \) (S4.22)
とすれば場合分けをせずに自動的に正の磁化を持つ格子だけが足し合わされます。この計算手順の理解を確認するために、図S4.25の3つの磁気モーメントを\(H_u-H_v\)グラフに配置し、式4.22によって磁化総量\(M\)を計算してみてください。対応する3つの格子のを1、それ以外では を0として計算を始めてください。正解を図S4.26と表4.6に載せておきます。
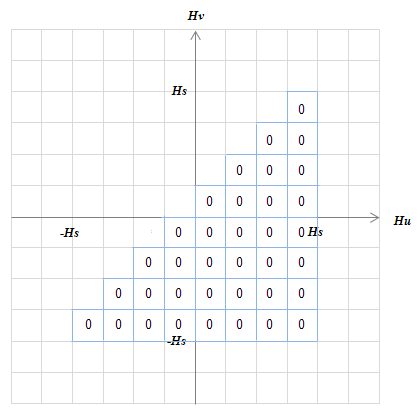 (a) 初期状態をすべての磁気モーメントが負の状態とする
(a) 初期状態をすべての磁気モーメントが負の状態とする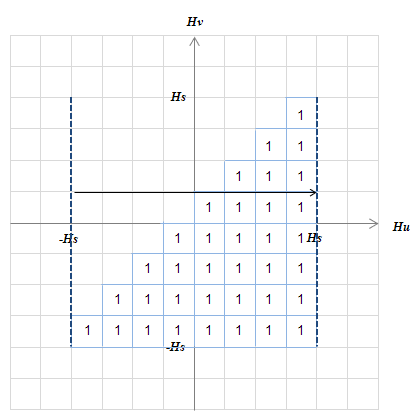 (b) \(H:-H_s→H_s\)
(b) \(H:-H_s→H_s\)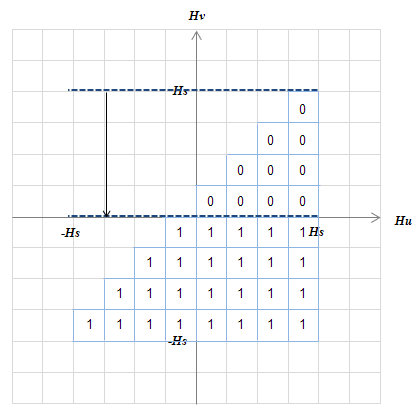 (c) \(H:H_s\)→0
(c) \(H:H_s\)→0図S4.24 入力\(-H_s→H_s→0\)に対する\(D(i,j)\)の変化
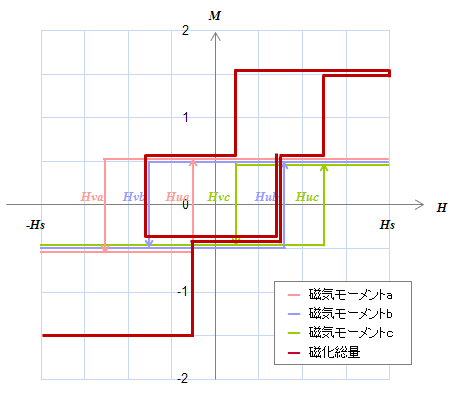 図S4.25 3つの磁気モーメント\(a,b,c\)
図S4.25 3つの磁気モーメント\(a,b,c\)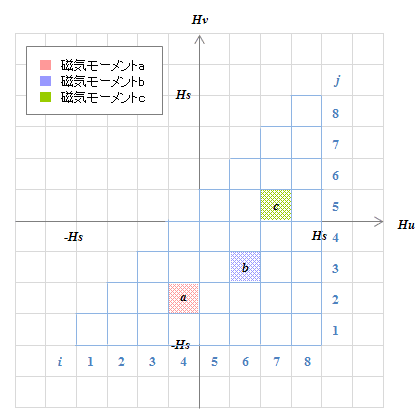 図S4.26 3つの磁気モーメントを\(H_u-H_v\)グラフに配置
図S4.26 3つの磁気モーメントを\(H_u-H_v\)グラフに配置図S4.25で定義した3つの磁気モーメント\(a,b,c\)をそれぞれ\(H_u-H_v\)平面に配置
| \(H\) | \(-H_s\) | 0 | \(H_s/2\) | \(H_s\) | 0 | \(-H_s/2\) | 0 | \(H_s/2\) |
| \(D(7,5)\) | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
| \(D(6,3)\) | 0 | 0 | 1 | 1 | 1 | 0 | 0 | 1 |
| \(D(4,2)\) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| \(M\) | -3/2 | -1/2 | 1/2 | 3/2 | 1/2 | -1/2 | -1/2 | 1/2 |
\(D(4,2)\)は磁気モーメント\(a、D(6,3)\)は磁気モーメント\(b\)、
\(D(7,5)\)は磁気モーメントcに対応する。初期磁化状態は-3/2とする。
少し気になること・・・
ところで、式(S4.22)によって入力\(H\)に応じた磁化総量が計算できることがわかりましたが、計算式の中に\(H\)が明示的に出てこないところが引っかかりますよね。プレイモデルの場合でも、現ステップと前ステップの\(H\)がヒステロンの引数になっていました((01) まずはプレイヒステロン 式S4.1参照)。プライザッハモデルの場合には、そのHになるまでの履歴情報を\(D\)が保持しているため、\(H\)を陽に持たなくても計算できるわけです。ただ、常に全ての格子の\(D\)を保持していなくてはならず、実はこれはプライザッハモデルの弱点になっています。
もう一つ、ギョッとするようなことをサラッっと言っておかなくてはいけません。ここまでの説明では入力\(H\)に対して磁化\(M\)を計算する方法を述べて来ました。一方、私たちの本来の目的は\(B\)を計算することです。もちろん、\(H\)と\(M\)がわかれば\(B\)が計算できるので理屈上の不都合はなく、そのようにしても良いのですが、磁界解析の世界では一般に、大胆にも、式(S4.20)の\(M\)を単に\(B\)に置き換える、という少々乱暴なことをやってしまいます。つまり、
\( B = \displaystyle \sum_{ 1 \leq i \leq B \\ 1 \leq j \leq i} K(i,j) D(i,j) \quad \cdots \) (S4.23)
とします。オイオイ、じゃあ、最初に出てきた磁気モーメントはどうなるんだ!って怒る人もいるかもしれませんが、まあまあ落ち着いて。いろいろな考え方があると思いますが、例えば、分布関数\(K\)に\(M\)から\(B\)への変換の役割も担わせれば式(S4.22)から(S4.23)への読み替えも可能になります。ただ、いずれにしても式(S4.22)と(S4.23)では\(K\)が異なり、本来であれば同じ文字を使うべきではないのですが、基本的な役割が同じで、今後\(M\)や式(S4.22)を扱うことはないので、式(S4.23)によって新たに\(K\)を再定義したいと思います。
今日は\(H_u-H_v\)グラフを使って磁化総量を計算する方法を見てきました。その途中で分布関数Kを導入しましたが、明日は、その\(K\)を材料特性から同定する方法についてお話します。
[*1] 一目瞭然でない人もいると思います。私の説明が稚拙なせいです。すみません。
私も、教科書や論文に”~であるからXXXは明らかである。”と書かれていると、 かなりの頻度でムカッとします、”どこが明らかなんだよ”って。一目瞭然ではない人は、お手数ですが、 下記コメント欄に”一目瞭然ではない”と書いて、ポチっと送信ボタンを押してください。