解析屋が見た損失評価

山田　隆

(03) 登場、”形状関数”

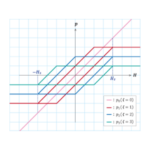
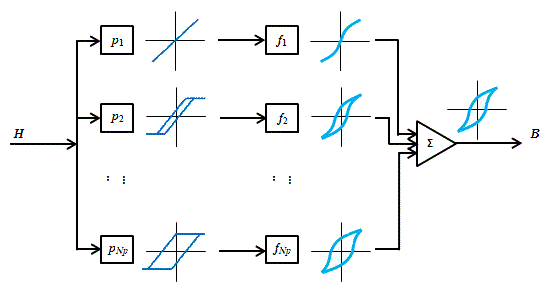
　ヒステロンを重ねることで”メジャーループ”や”マイナーループ”みたいなものが作れることがわかりました。 しかし、良く見ると、そこには材料特性が反映されていません。 唯一、飽和磁界\(H_s\)が使われていますが、これは\(p\)の動作範囲を規定しているだけで、出力となる\(B\)には影響を与えません。 ヒステロンの定義式(式S4.1)を見ると、ヒステロンは\(H\)の次元を持っていて、位相差(\(±e\))はあるものの、相変わらず\(H\)のようなものであることがわかります。 これでは\(H\)と\(B\)を関係付ける磁化モデルとして使い物になりませんから、\(p\)を\(B\)に変換する必要があります。 そのために、プレイモデルでは”形状関数”というものを導入します。 この形状関数\(f_n\)はヒステロン毎に与えられ、その和が\(B\)になるように決められます。 すなわち、

\( B = \displaystyle \sum_{n}f_n(p_n(H)) \quad \cdots \) (S4.6)

　前回の式S4.4と比べてみてください。 式S4.4ではヒステロンをそのまま足し合わせていましたが、式S4.6では、形状関数によってヒステロンを変換した後に足し合わせています(図S4.8)。形状関数が\(H\)が\(B\)に変換すると同時に、材料の特性をプレイヒステロンに持たせています。
　ここで\(f_n\)は\(p_n\)だけの関数であることに注意してください。形状関数\(f_n\)は\(p_n\)以外のヒステロンの影響は受けませんし、ヒステロン値\(p_n\)が同じ点は同じ変換を受けます(図S4.9)。 このことから各ヒステロンの上辺と下辺は変換後も直線になることがわかります。
　では、この形状関数の効果を見てみましょう。ここでは簡単のために\(f_n\)は各ヒステロンの高さだけを変える変換だとしましょう。つまり、\(c_n\)を定数として

\( f_n(p_n) =c_n*p_n \quad \cdots \) (S4.7)

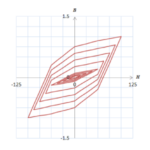
です。定数{\(c_n\)}を変えた場合に、式S4.6で計算される\(B\)がどのような軌跡になるかを図S4.10に示します。軌跡の描き方はヒステロンだけの場合と全く同じです。図S4.10(a)は{\(c_n\)}を全て同じにした場合です。この時のループ形状は、ヒステロンだけの場合と相似形になります。そこから、\(c_0\)から\(cN_p-1\)に向けて大きくしたものが(b)、小さくしたものが(c)です。この定数｛\(c_n\)｝、すなわち{\(f_n\)}を変えることでループの形状をコントロールできることがわかると思います。この特性を使って、実際の材料の特性を捉えるように{\(f_n\)}を決めていきます。

図S4.8　プレイモデルと形状関数の足し合わせダイアグラム<Ⅱ>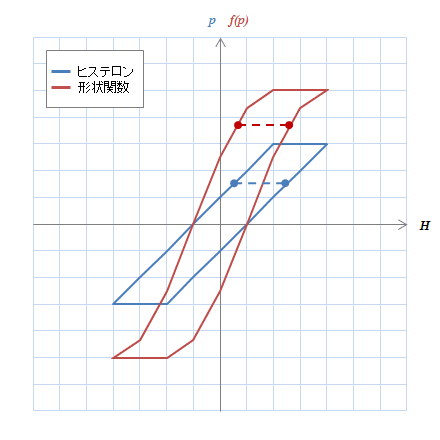

図S4.9　ヒステロン(\(\zeta=1\))と形状関数

同じヒステロン値の点は同じ形状関数値に写される。

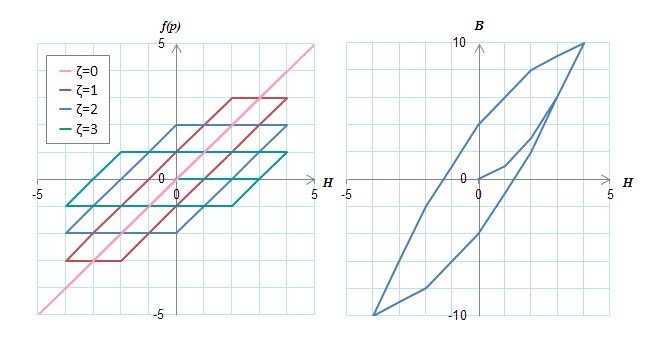(a)定数\(c_n\)を一定\((c_0=c_1=c_2=c_3=1)\)としたときのヒステロン(左)と\(BH\)の軌跡(右)

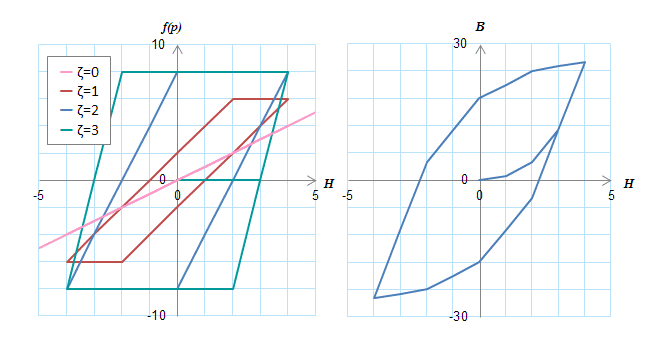(b)定数cnを一定\((c_0=1, c_1=2, c_2=4, c_3=8)\)としたときのヒステロン(左)と\(BH\)の軌跡(右)

幅の広いヒステロンの寄与度を上げることでBHの軌跡も幅広くなる。

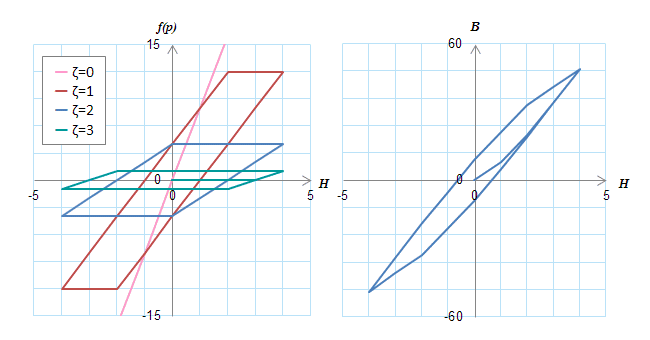(c)定数cnを一定\((c_0=8, c_1=4, c_2=2, c_3=1)\)としたときのヒステロン(左)と\(BH\)の軌跡(右)

幅の広いヒステロンの寄与度を下げることで\(BH\)の軌跡も閉じてくる。

単純な形状関数であっても\(BH\)の軌跡を大きく変化させることができる。

(04) 形状関数に表現力を！

　形状関数の効果が実感できたところで、形状関数についてもう少し細かく見てみましょう。 上で見たように定数であそこまで制御できるのですから、形状関数の表現力を上げればもっと細かい調整ができ材料特性の再現性を上げることができそうです。プレイモデルではそのために、ヒステロン上に等間隔の節点を設け、その間を次のように線形に補間します(図S4.11)。

\( f_n(p) = f_n(p_{n,m-1})+\mu(n,m)*(p-p_{n,m-1}) \quad \cdots \) (S4.8)

　ここで、\(p_n,m\)はヒステロン\(p_n\)上の\(m\)番目の節点、\(μ(n,m)\)は注目しているpを挟む2つの節点\(p_n,m-1\)と\(p_n,m\)の間の\(f_n\)の傾きで

\( \mu(n,m)=\frac{f_n(p)-f_n(p_{n,m-1})}{p-p_{n,m-1}} \quad \cdots \) (S4.9)

となります。 式中に\(n\)と\(m\)がたくさん現れて少々煩わしいのですが、式S4.8、S4.9はヒステロン毎に行われ、”ヒステロン間の補間はありません”ので実は単純です。 節点はヒステロン毎に\((‐H_s、H_s)\)の間を等分割しますが、分割幅\(\Delta p\)は

\( \Delta p = 2H_s/N_p \quad \cdots \) (S4.10)

とします。この節点をいつものヒステロンのグラフ上に配置すると図S4.12のようになり、ある1つのヒステロンに注目して\(f\)への変換の様子を描くと図4.13のようになります。

このように形状関数を決めて節点の数を増やしていけば、どんな\(BH\)ループでも表現できるような希望が湧いてきませんか？湧いてこない！？もっと夢と希望を持ちましょう。

　プレイモデルでは、材料毎に節点上の\(f_n(p_n,m)\)を決めて材料特性をモデルに持たせます。これについては次回に続くとしましょう。

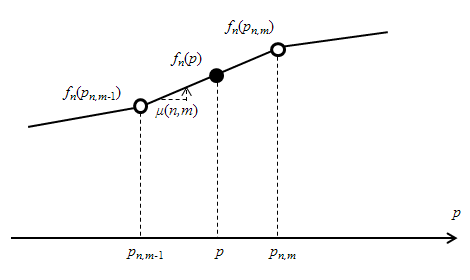図S4.11　形状関数の補間

ヒステロン\(p_n\)上の2つの節点\(p_n,m-1\)と\(p_n,m\)の間の点\(p\)における形状関数値は、
節点値\(f_n(p_n,m-1)\)と\(f_n(p_n,m)\)から線形補間される。その2点間の傾きが\(\mu(n,m)\)である。

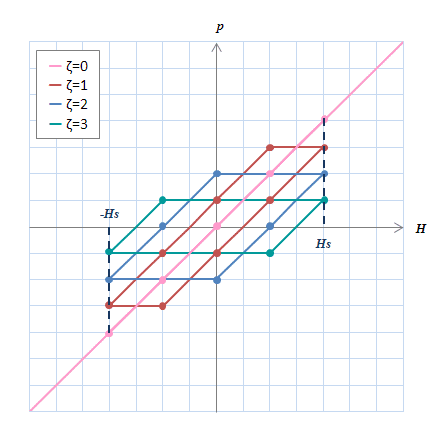図S4.12　ヒステロン上の節点の配置の様子

区間\((‐H_s、H_s)\)を\(N_p\)分割した\(H\)(この例では-4,-2,0,2,4)に対応するヒステロン上節点が配置される。
隣り合うヒステロンの節点は\(p\)方向には互い違いになっている。

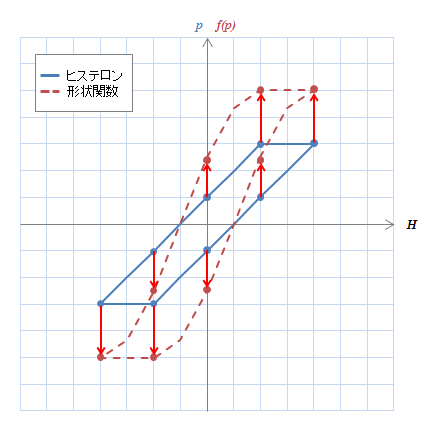図S4.13　節点と補間によって表現された形状関数

節点を増やすことによって形状関数の表現力が高くなる。