解析屋が見た損失評価 夏休み補講編
山田 隆
(07) 同定作業開始!
いよいよ同定をしてみましょう。この手順は面倒ですが、実際にはソフトウェアがやってくれますので心配しないでください。ただ、プレイモデルの仕組みを理解するためには一度具体的にやっておくことはとても大事です。今日もたくさん手を動かしましょう。
この説明では簡単のために図S4.16のような2本のメジャーループが与えられているとします。この場合、ヒステロンは4本で、節点の総数は23ありますが、形状関数は\(p\)にしかよらないこと、ヒステロンが上下対称であることから、決めるべき節点上の形状関数の個数は8個になります。ただ、上でも述べたとおり、直接扱うのはfではなく\(f\)の傾きを表す\(\mu(n,m)\)で、同定すべき\(\mu(n,m)\)は6個になります(図S4.17)。これを表の形にまとめると表S4.4のようになります。この表の\(\mu(n,m)\)をすべて埋めることが同定作業のゴールになり、それができればプレイモデルは完成です。
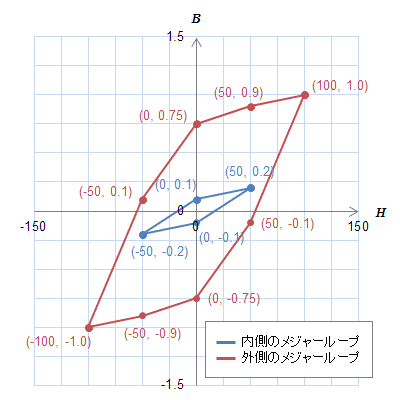 図S4.16 同定に使う2本のメジャーループ(\(H_s=100、\Delta H=50\))
図S4.16 同定に使う2本のメジャーループ(\(H_s=100、\Delta H=50\))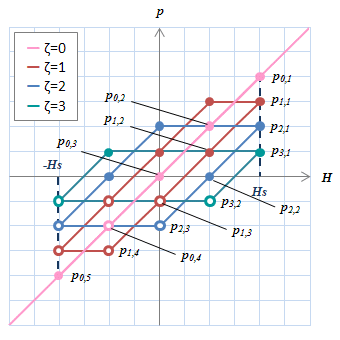 (a)ヒステロン上に配置された節点
(a)ヒステロン上に配置された節点ヒステロン上に節点番号\(p_n,m\)を示した。総数は23だが、上下対称性から同定すべき節点は上半分(または下半分)だけになり、さらに、\(p\)が同じ値をもつ側辺上の2点は共通の\(f\)値を持つため、同定すべきfの節点値の数は8になる。
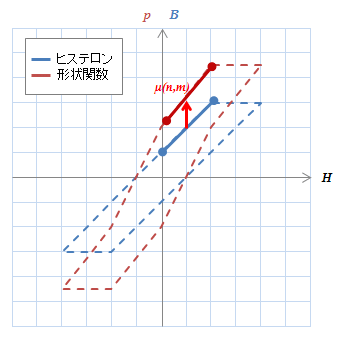 (b)同定すべき\(\mu(n,m)\)
(b)同定すべき\(\mu(n,m)\)節点値\(f_n(n,m)\)が同定するために、節点値間の形状関数の傾き\(\mu(n,m)\)を同定する。
図S4.16の2本のメジャーループが与えられた場合、使用するヒステロンは4つになり、
その上の23の節点の形状関数が決まればプレイモデルが完成する。
同定をするために、図S4.16のメジャーループはプレイモデルの定義式(S4.6)に従って、形状関数の足し合わせで再構成できると仮定します。そして、それぞれの\(H\)の区間におけるメジャーループの変化量と各ヒステロンの動作状況を見比べながら、その区間における\(\mu(n,m)\)をあぶりだしていきます。
まず、外側のメジャーループの動きを再現してみましょう。前々回やったように手を動かしましょう。今回もワークシートを用意しました(PDF 40KB)。動作点はメジャーループ状をぐるぐる回っているわけですが、ここではメジャーループの最大振幅の点を説明の出発点とします。ここからΔHだけHを減少させます。このとき、\(p_0\)以外のヒステロンは水平に動きますので、メジャーループのBの変動分はf0の変動分、つまり、\(\mu(0,1)\)になります(図S4.18)。式で書くと
\( B~1_1 – B~1_2=\mu(0,1) \quad \cdots \) (S4.15)
ここでの\(\mu\)は\( \mu (n,m) = \mu(n,m) \times (p_{nm}-p_{n,m-1})\)追加とする。
となります。ここでBijはi番目(最外を1とする)のメジャーループ上のj番目(右上を1として反時計方向に進む)の節点のBの値です。前回のお話ではm(0,1)をBHカーブから求めましたが実際にはこのようにしてメジャーループから求めます。HをさらにΔHだけ減少させましょう。ここではメジャーループの減少幅が大きくなっていますが、これはp1が参加した効果であることがわかります。ただ、残念ながら
\( B^1_2 – B^1_3 = \mu(0,2)+\mu(1,1) \quad \cdots \) (S4.16)
ですので、Bの変化量だけではp0とp1の寄与は決められません(図S4.19)。困りました。そこで、内側のメジャーループに注目します。上と同様に見ると、最高点から次の点までのBの変化分はp0だけがになっていることがわかります(図S4.20)。つまり、
\( B~2_1 – B^2_2 = \mu(0,2) \quad \cdots \) (S4.17)
ですから、これは式(S4.16)に代入するとm(1,1)が次のように計算できます。
\( \begin{eqnarray}\mu(1,1) &=& B^1_2 – B^1_3 – \mu(0,2) \\ &=& B^1_2- B^1_3 – (B^2_1 – B^2_2)\end{eqnarray} \quad \cdots \) (S4.18)
おお、ワンダフルワールド!同様に、例えば\(\mu(2,1)\)も
\( \mu(2,1) = B^1_3 – B^1_4 – (B^2_2 – B^2_3) \quad \cdots \) (S4.19)
のように計算できます。それ以外も、同じような手続きで求めることができます。皆さん、頑張って計算して表S4.4を埋めましょう。
ところで、上のような計算が成り立つのはヒステロンがある区間で一定値になる性質があるからです。それによって、ある区間において特定のヒステロンの変化量だけを抽出することが可能になっています。その様子を見るためにそれぞれのループの軌跡における各ヒステロンの動作状態を表S4.5にまとめます。ヒステロンの変化がある場合を1、ない場合を0としています。この動作状態を組み合わせることで、特定のヒステロンの変化量をあぶりだせることがわかると思います。
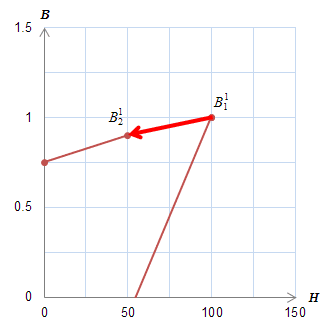 (a)メジャーループ上の\(B\)の変化
(a)メジャーループ上の\(B\)の変化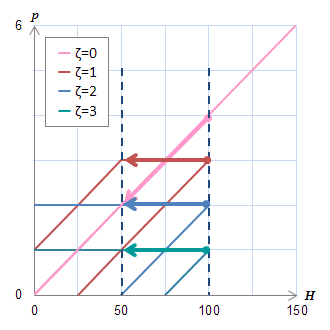 (b)ヒステロンの動き
(b)ヒステロンの動き図S4.18 区間(100、50)における外側のメジャーループ上の\(B\)の変化(a)と各ヒステロンの動き(b)
この区間における\(B\)の変化に寄与しているのはヒステロン\(p_0\)のみであることがわかる。
 (a)メジャーループ上の\(B\)の変化
(a)メジャーループ上の\(B\)の変化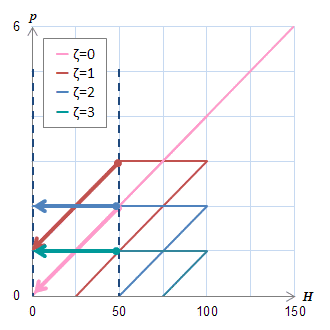 (b)ヒステロンの動き
(b)ヒステロンの動きこの区間のB変化には\(p_0\)と\(p_1\)の両方が寄与している。
外側のメジャーループ上を動く場合には、ヒステロンへの入力の\(H\)が\(H_s\)に達するために、
\(p_1\)の下降が\(H=50\)で始まることに注意する。
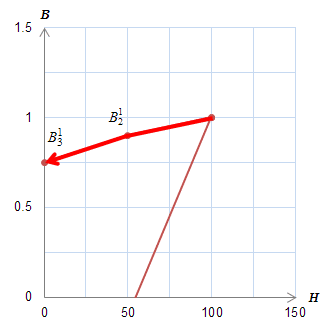
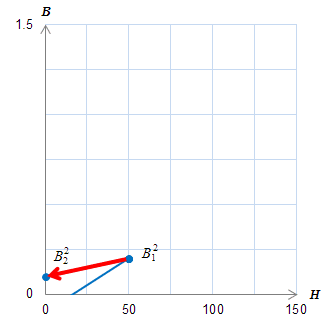 (a)メジャーループ上の\(B\)の変化
(a)メジャーループ上の\(B\)の変化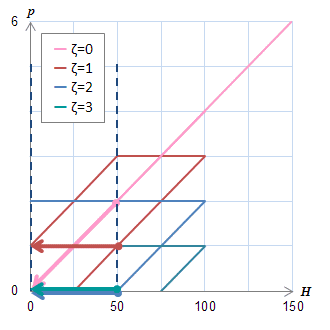 (b)ヒステロンの動き
(b)ヒステロンの動きこの区間における\(B\)の変化に寄与しているのはヒステロン\(p_0\)のみであることがわかる。
内側のメジャーループ上を動く場合には、\(H\)の最大値が50であるために、
\(p_1\)の下降が\(H=0\)まで始まらずBの変化には寄与しない。
| \(pの区間 \setminus p_i\) | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) |
| 4~3 | \(\mu(0,1)\)
0.1
|
|||
| 3~2 | \(\mu(1,1)\) | |||
| 2~1 | \(\mu(0,2)\) | \(\mu(2,1)\) | ||
| 1~0 | \(\mu(1,2)\) | \(\mu(3,1)\) | ||
| 0~-1 | \(\mu(0,3)\) | \(\mu(2,2)\) | ||
| -1~-2 | \(\mu(1,3)\) | |||
| -2~-3 | \(\mu(0,4)\) | |||
| -3~-4 |
各ヒステロンの節点間の傾き\(\mu(n,m)\)を\(H\)をある区間で変化させ、
その時のメジャーループの変化量とヒステロンの動作状況から求める。
(1 : ヒステロンが変化する, 0: ヒステロンが変化しない)
| \(Hの区間 \setminus p_i\) | ループの位置 | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) |
| 100 → 50 | 外 | 1 | 0 | 0 | 0 |
| 内 | 0 | 0 | 0 | 0 | |
| 50 → 0 | 外 | 1 | 1 | 0 | 0 |
| 内 | 1 | 0 | 0 | 0 | |
| 0 → -50 | 外 | 1 | 1 | 1 | 0 |
| 内 | 1 | 1 | 0 | 0 | |
| -50 → -100 | 外 | 1 | 1 | 1 | 1 |
| 内 | 0 | 0 | 0 | 0 | |
| -100 → -50 | 外 | 1 | 0 | 0 | 0 |
| 内 | 0 | 0 | 0 | 0 | |
| -50 → 0 | 外 | 1 | 1 | 0 | 0 |
| 内 | 1 | 0 | 0 | 0 | |
| 0 → 50 | 外 | 1 | 1 | 1 | 0 |
| 内 | 1 | 1 | 0 | 0 | |
| 50 → 100 | 外 | 1 | 1 | 1 | 1 |
| 内 | 0 | 0 | 0 | 0 |
(08) プレイモデルまとめ
これでプレイモデルも完成です。どうでしょう、プレイモデルの仕組みは理解いただけたでしょうか?解説が少し長くなりましたので、簡単にまとめておきましょう。
- 任意のマイナーループを表現するための磁化モデル。
- ヒステロンと形状関数によって構成されている。
- モデルの同定は測定されたメジャーループ群を使って行われる。
- ヒステロンは入力のHに位相遅れを与え、マイナーループの”素”を作る。
- 位相遅れ量(幅)の異なる複数のヒステロンを組み合わせることで諸々のマイナーループを表現できるようになる。
- ヒステロン自体は飽和磁界を除き材料の特性を持たない。
- 形状関数は材料の磁化特性を表現する。
- 形状関数はヒステロン毎に別々に定義され、それぞれのヒステロン値のみの関数になっている。
- 形状関数はヒステロン上の節点値とその間を線形補間する関数で定義される。
- 節点の値は、測定されたメジャーループ群から同定される。
- 隣合うメジャーループの振幅は等間隔になるように測定される。振幅の最大値は飽和磁界である。
- メジャーループ間の振幅間隔がマイナーループを捉える分解能になり、メジャーループの数の2倍のヒステリシスループが生成される。
- メジャーループの局所的な変化と、その際のヒステロンの変動の関係から形状関数が同定される。
不明な点があれば遠慮なくお問い合わせください。最初にも書きましたが、プレイモデルの難しさは手続きの多さにあると思います。面倒くさがっていては理解が進みません。ステップを踏んで手を動かしながら体に馴染ませていけば理解も進むと思います。技術の習得には努力が必要なことは不変の真理のようですね。
プレイモデルの説明は一通り終えましたが、他の多くの解説ではプライザッハモデル基に説明されることが多いようですので、この解説でも最後にプライザッハモデルとの関係について触れておきたいと思います。これについては来週にしましょう。